The determination of the gravity field of the Earth represents one of the three pillars of geodesy. Global gravity field solutions for the long and medium wavelengths are today derived from satellite observations, mainly of the three dedicated gravity field missions CHAMP, GRACE and GOCE. The estimation of gravity field parameters to model this major force acting on the satellites thereby is closely related to the determination of precise satellite orbits. Precise orbits are not only needed to geo-locate the observations of the instruments onboard the satellites dedicated to the gravity field determination, i.e., the K-Band microwave data in case of GRACE, or the gradiometer data in case of GOCE, but the GPS data themselves contain information about the long wavelength part of the gravity field.
Despite the long history in precise orbit determination at AIUB as a member of the Center for Orbit Determination in Europe (CODE) the adaption of the orbit model for the GRACE satellite posed a special challenge due to the fact that the GRACE orbits are very actively controlled by a number of cold gas thrusters to maintain the fine pointing of the satellites that is a prerequisite for the flawless working of the microwave link. Meyer et al. (2012) studied the impact of the thruster pulses on the reduced dynamic satellite orbits of GRACE and confirmed the importance of the corresponding observed accelerations for gravity field determination.
Combined solutions from GRACE GPS and K-Band range-rate observations on the one hand, and from GOCE GPS and gradiometer data on the other hand, were determined at AIUB. For the GOCE gradiometer processing Jäggi et al. (2011) studied two-step procedures to take into account the colored noise of the gradiometer data for gravity field determination. In a first step normal equations based on each of the diagonal components of the gravity tensor were set up for the spherical harmonic (SH) coefficients. In addition also empirical piecewise linear parameters were set up for the gradiometer observables at one minute intervals. An inversion of the associated normal equations provided so-called “free solutions” for the SH coefficients and for the empirical parameters. In a second step either the gradiometer residuals or the estimated piecewise linear parameters from the first step were used to derive empirical covariances that were taken into account in the second step to further improve the gravity field estimates. Essentially the same performance could also be achieved within one step by constraining differences between consecutive parameters of the empirical piecewise linear gradiometer model. Irrespective of the actually used method, absorption of high frequency signal content of the gravity field by the piecewise linear parameters could be avoided.
The GOCE gradiometer observable is sensitive to the fine structure of the gravity field, but due to the band-limitation at low frequencies the coefficients of the gravity field at degrees smaller than about 30 are determined mostly from GPS (Fig. 1, left). In Fig. 1 (right) the combination of GRACE and GOCE gravity fields is illustrated with respect to the gravity field model GOCO03S. At low to medium degrees the GRACE solution is superior due to the high sensitivity of the K-Band observable even at low frequencies. Above degree 110 the combination is dominated by the GOCE gradiometer observable. The effect of the badly determined zonal coefficients is excluded in Figs. 1 and 2 by the use of degree medians instead of degree variances.
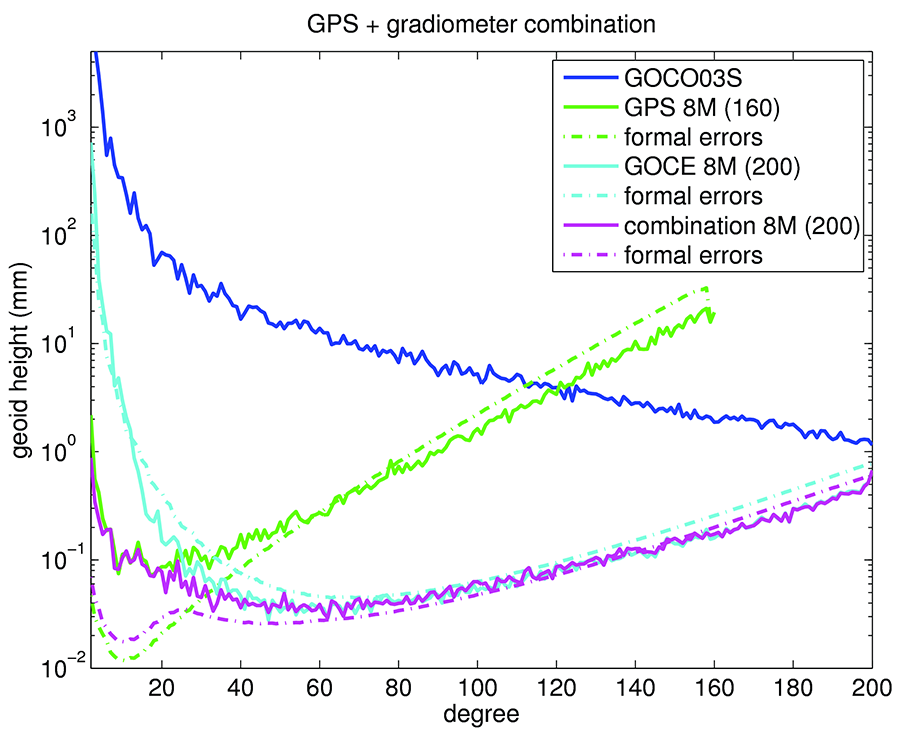 Difference degree medians between GOCE GPS-only, gradiometer-only, and combined GPS/gradiometer gravity field coefficients and the reference field GOCO03S.
Difference degree medians between GOCE GPS-only, gradiometer-only, and combined GPS/gradiometer gravity field coefficients and the reference field GOCO03S.
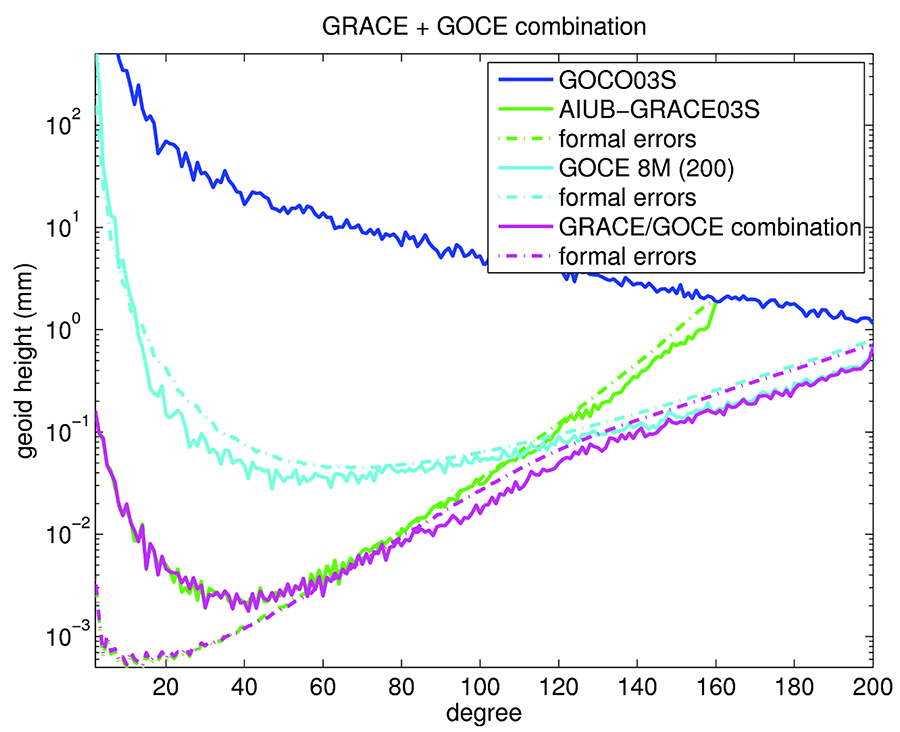 Difference degree medians of GRACE-only, GOCE-only, and combined GRACE/GOCE gravity field coefficients relative to GOCO03S.
Difference degree medians of GRACE-only, GOCE-only, and combined GRACE/GOCE gravity field coefficients relative to GOCO03S.
Apart from the improved sensitivity to small scale (high degree) features of the gravity field the combination of GRACE and GOCE observations has another major advantage compared to GRACE-only solutions. Due to the one-dimensional observation geometry of the GRACE K Band observable the spherical harmonic coefficients at certain orders suffer from aliasing of slowly varying gravitational signals, e.g., of tidal origin. In the triangle plot the concerned coefficients are visible as vertical stripes (Fig. 2, left) afflicted from increased noise. By combination with GOCE data this problem is cured (Fig. 2, right), even for medium degree coefficients that are still dominantly determined from the GRACE K-Band observations.
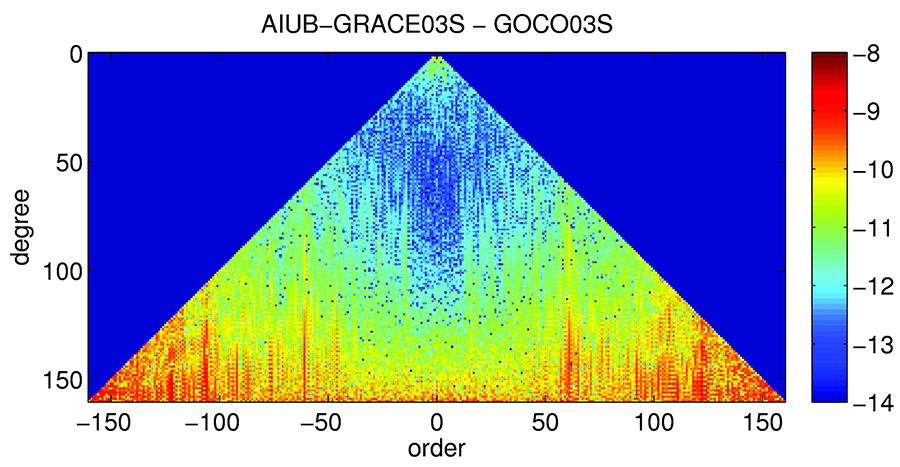 Triangle plot of the differences between sin- (left part of triangle) and cos-coefficients (right part of triangle) of the seven year GRACE gravity field solution AIUB-GRACE03S and GOCO03S.
Triangle plot of the differences between sin- (left part of triangle) and cos-coefficients (right part of triangle) of the seven year GRACE gravity field solution AIUB-GRACE03S and GOCO03S.
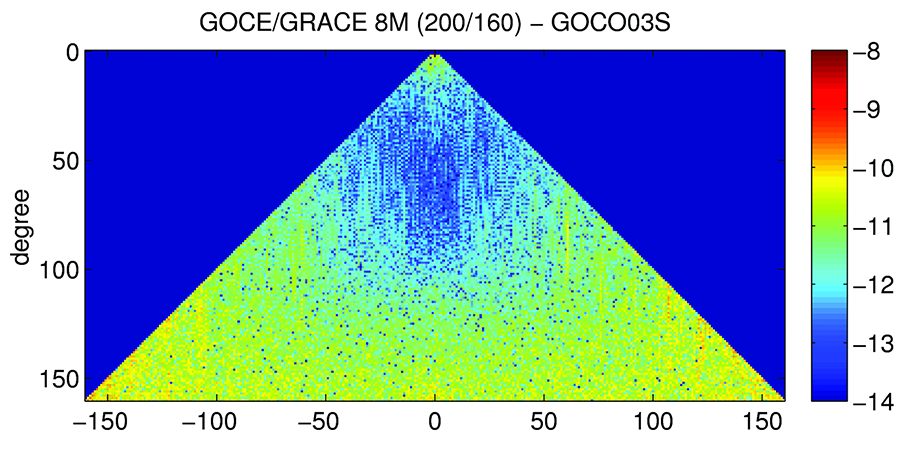 Differences between the spherical harmonic sin- and cos-coefficients of a combined solution of AIUB-GRACE03S and eight months of GOCE gradiometer data compared to GOCO03S.
Differences between the spherical harmonic sin- and cos-coefficients of a combined solution of AIUB-GRACE03S and eight months of GOCE gradiometer data compared to GOCO03S.
References
Jäggi, A., G. Beutler, U. Meyer, L. Prange, H. Bock, R. Dach, L. Mervart; 2011: Gravity Field Determination at AIUB: From CHAMP and GRACE to GOCE. EGU General Assembly 2011, Vienna, Austria, April 3-8, 2011.
Meyer, U., Jäggi, A., Beutler, G. (2012) The Impact of Attitude Control on GRACE Accelerometry and Orbits. In: Geodesy for Planet Earth, edited by S. Kenyon, M.C. Pacino, and U. Marti, 136: 139-146, ISBN 978-3-642-20337-4, doi: 10.1007/978-3-642-20338-1_17.