Estimating the Geocenter coordinates
Geocenter motion can results from the variation of the center of mass of the entire Earth system, i.e., the solid Earth with oceans and the atmosphere, with respect to the origin of the reference frame. The reference frame is realized by long-term satellite observations provided by a network of ground stations. The artificial Earth satellites orbit around the instantaneous center of mass of the Earth in the inertial reference frame. Thus, a transformation between the inertial frame, defined by satellites, and the instantaneous Earth-fixed frame, realized by a global network of observing stations, provides the information about the geocenter motion. The geocenter may mathematically be realized by the no-net-translation minimum constraint condition of the Helmert transformation imposed on a sub-set of stable fiducial stations that have well-established coordinates in the a priori reference frame.
In theory, all satellite geodetic techniques should be able to recover the geocenter coordinates. Observations from Global Navigation Satellite Systems (GNSS) and Doppler Orbitography and Radiopositioning Integrated by Satellite (DORIS) can be used for the determination of the equatorial X and Y components of geocenter motion. They are, however, not well suitable to recover the Z-coordinate of the geocenter due to the correlation with orbit parameters related to the solar radiation pressure modelling (e.g., Meindl et al., 2013, Kosek et al., 2014). SLR is nowadays the only technique that is fully capable of recovering the geocenter coordinates. The advantage of the SLR technique lies in the observation principle that is based on very short and precise laser pulses. Averaged over a certain time span, SLR measurements are precise to a few millimeters. Moreover, SLR benefits from the simple construction of passive satellites, like LAGEOS. The geodetic SLR satellites are dense and spherical in shape and have greatly minimized area-to-mass ratios which also minimize the orbit perturbation related to non-gravitational forces, e.g., the atmospheric drag and solar radiation pressure.
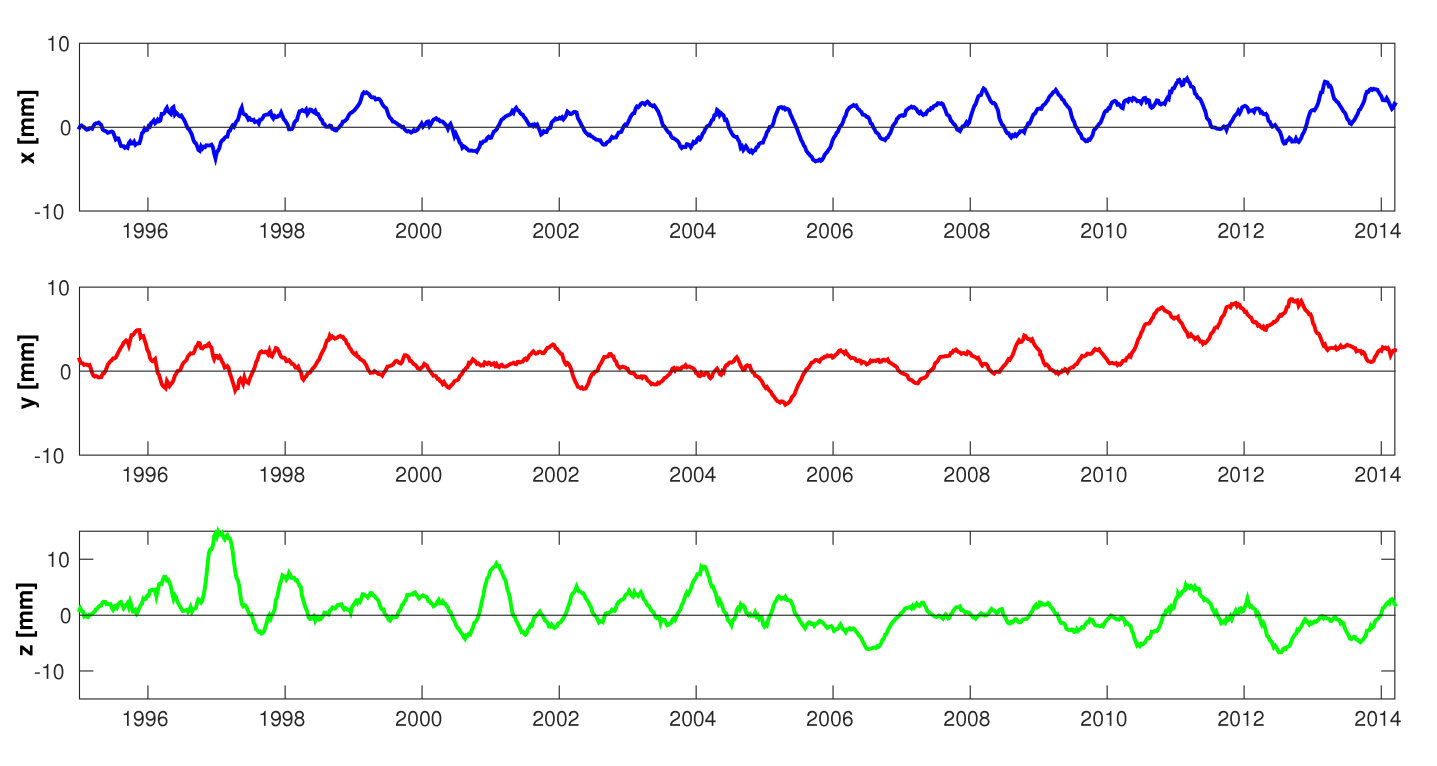Geocenter coordinates derived from SLR observations filtered using a 3-month sliding window of the Savitzky-Golayfilter.
The figure shows the time series of geocenter coordinates derived from 7-day SLR solutions using observations to LAGEOS-1/2, Starlette, Stella, and AJISAI. The series is filtered using a 3-month sliding window of the Savitzky-Golay filter. The series shows seasonal variations with a mean amplitudes of 3, 2, and 4 mm for the X, Y, and Z components, rescpectively. However, the amplitudes vary for different periods. Until 2008 the mean offset of all geocenter components is below 1 mm and the slopes do not exceed 0.15 mm/year. This implies that the analysis is consistent with the a priori reference frame ITRF2008 that is based on observations collected until 2008. In the period 2011-2013, the Y component shows a systematic shift of +4 mm and the Z component of -2 mm. Matsuo et al. (2014) associate these shifts with the accelerated ice mass depletion in Greenland and West Antarctica, which should introduce a slope of -0.17, +0.37, -0.56 mm/year for the X, Y, and Z component, respectively. The origin of future reference frames should be aligned to the mean Earth’s center-of-mass and, thus, it should be adapted to the processes related to the climate change.
Estimating Earth rotation parameters
The Earth rotation parameters (ERPs, i.e., X and Y pole coordinates and UT1-UTC or its first derivative in time denoted as Length-of-Day, LoD) define, along with the precession and nutation parameters, the transformation from the Earth-fixed to the inertial frame through a transformation matrix. Polar motion and LoD values can be derived from all space-geodetic techniques, whereas UT1-UTC can only be derived from VLBI or Lunar Laser Ranging observations due to the direct correlation between UT1-UTC values and satellites’ ascending nodes.
To assess the quality of SLR-derived ERPs, we generate three solutions using: (1) SLR observations to LAGEOS-1/2, (2) SLR observations to Starlette, Stella, and AJISAI (here called SLR-LEO), and (3) using all 5 satellites (here called multi-SLR). ERPs are mathematically computed through the no-net-rotation minimum constraint condition of the Helmert transformation imposed on a sub-set of stable fiducial stations. We compare SLR-derived ERPs with the IERS-08-C04 series (Gambis, 2004) for the 7-day SLR solutions with and without co-estimating geopotential coefficients up to degree/order 4/4 (Sośnica et al., 2014). In the LAGEOS-1/2 solutions and in the multi-satellite SLR solutions without estimating the geopotential, the once-per-revolution empirical orbit parameters in the out-of-plane direction (WS/WC) are additionally estimated because they absorb large variations of C20 (Sośnica et al., 2012). Not estimating WS/WC parameters leads to inferior SLR solutions when C20 is not solved for.
The current accuracy of SLR-derived polar motion, assessed by means of the weighted RMS (WRMS) w.r.t. the IERS-08-C04 series, is at the level of 118-149 µas, which corresponds to 4 to 5 mm on the Earth’s surface. The WRMS of SLR-derived LoD values, when the gravity field parameters are simultaneously estimated, is 56 µs/day, corresponding to about 26 mm on the Earth’s surface. The mean bias of SLR-derived LoD parameters w.r.t. IERS-08-C04 is 6.3 µs/day, corresponding to 3 mm on the Earth’s surface. In the LAGEOS solutions, the mean biases w.r.t. IERS-08-C04 for the X and Y pole coordinates are larger in the solution when no geopotential parameters are estimated. In the LAGEOS solutions with estimating geopotential coefficients, the shift amounts to 4.1 and -8.0 µas for the X and Y pole coordinate, respectively. In the LAGEOS solutions without estimating geopotential parameters these shifts are 45.8 and -54.1 µas. A particular degradation of LoD estimates is observed for the solution without estimating geopotential parameters, namely the WRMS increases from 57.0 to 120.5 µs. LoD absorbs the part of C20 that is not accounted for by a priori C20 values in the solution without estimating geopotential, which leads to a shift in LoD series (Sośnica 2014). As a result, the C20 estimates and the shift of LoD from the solution without estimating the geopotential are of the same order of magnitude. Thus, the estimation of C20 is beneficial for the LAGEOS solutions when estimating LoD values.
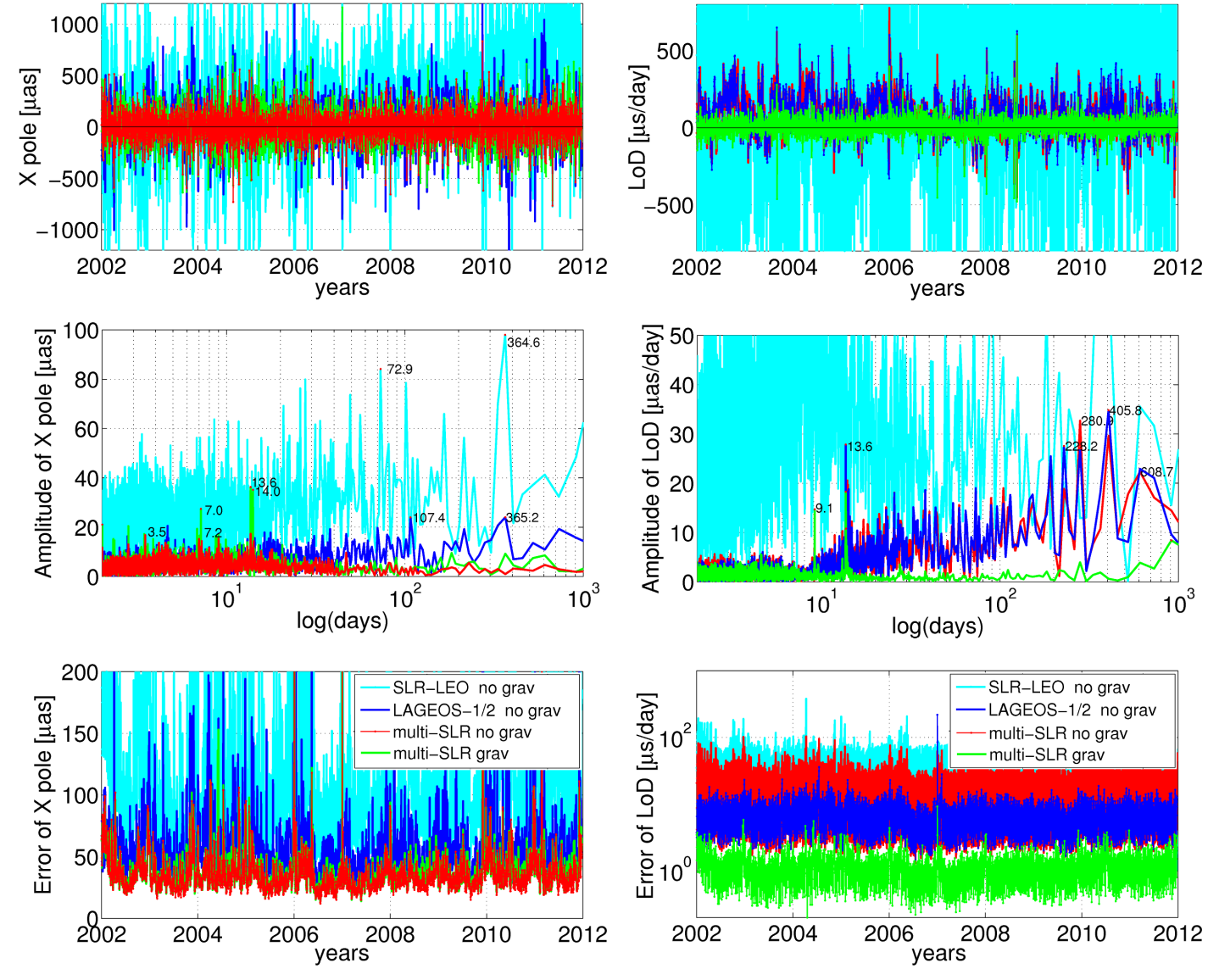Left: Differences of the X pole coordinate w.r.t. IERS-08-C04 series (top), spectral analysis of the differences (middle), a posteriori errors of the X pole coordinates (bottom). The Y pole coordinate shows similar variations, thus, it is not shown here.
Right: Differences of the LoD w.r.t. IERS-08-C04 series (top), spectral analysis of the differences (middle), a posteriori errors of LoD estimates (bottom). Note the logarithmic scale for the y axis in the bottom figure.
The estimation of Earth's gravity field parameters is beneficial for low orbiting SLR satellites when a static a priori gravity field model is used. The degradation of pole coordinates is significant in the SLR-LEO solutions, which is reflected in the WRMS of 267.9 and 437.5 µas for the X pole coordinate in the solutions with and without estimating the geopotential, respectively. The Figure shows the X pole coordinates (left side plots) and shows LoD estimates (right plots) as differences w.r.t. the IERS-08-C04 series for different SLR solutions. The LAGEOS solution without estimating gravity field parameters is closest to the official ILRS solutions. The figure above clearly shows that including low orbiting satellites is beneficial for ERP estimation.
Both, the multi-SLR solutions with and without estimating gravity field parameters have a similar quality and a posteriori errors of pole coordinates at a similar level, which are much smaller as compared to LAGEOS-1/2 solutions. However, the plot in the middle on the left hand side shows peaks at about 3.5, 7.0, and 14.0 days, which are related to the lengths of the solution batches or to the orbit alias with tidal waves in the multi-SLR solutions with co-estimating the geopotential terms. The plot shows that all multi-SLR solutions (regardless whether estimating the geopotential or not) reduce the peaks in the X pole coordinate that are apparent in the LAGEOS-1/2 solutions. These peaks are related to LAGEOS orbit modeling deficiencies or to the alias with tidal waves, e.g., the annual signal and an eclipsing period of LAGEOS-2 (about 111 days).
Regarding LoD, the simultaneous estimation of the gravity field parameters reduces the offset of LoD estimates (the top plot on the right hand side). Further, the peaks in the spectrum analysis are reduced (middle plot on the right hand side), which correspond, e.g., to orbit modeling deficiencies (peaks of 222 days - a draconitic year of LAGEOS-2, of 280 days - an eclipsing period of LAGEOS-1). The co-estimation of geopotential parameters substantially reduces the a posteriori error of estimated LoD (bottom plot no the right hand side). The a posteriori error of LoD in the multi-SLR solutions (16.9 µs/day) is more than factor of two higher than in the LAGEOS-1/2 solutions (7.1 µs/day) when the gravity field parameters are not estimated. This difference implies that the estimation of the gravity field parameters is essential for high-quality LoD estimates when using SLR data to low orbiting geodetic satellites.
Related references providing further details and results.
Gambis, D. (2004). Monitoring Earth orientation using space-geodetic techniques: state-of-the-art and prospective. J Geod 78(4-5): 295-303, doi: 10.1007/s00190-004-0394-1.
Kosek, W., Wnęk, A., Zbylut-Górska, M., Popiński, W. (2014). Wavelet analysis of the Earth center of mass time series determined by satellite techniques. J Geodyn 80: 58-65.
Matsuo, K., Otsubo, T., Munekane, H., Fukuda, Y. (2013). Geocenter motion excited by large-scale mass redistribution. Proc. of the 19th International Workshop on Laser Ranging, Annapolis, Oct 27-31, 2014.
Meindl, M., Beutler G., Thaller, D., Dach, R., Jäggi, A. (2013). Geocenter coordinates estimated from GNSS data as viewed by perturbation theory. Adv. Sp. Res 51(7): 1047-1064.
Sośnica, K., Thaller, D., Dach, R., Jäggi, A., Beutler G. (2012). Sensitivity of Lageos Orbits to Global Gravity Field Models. Artificial Satellites 47(2): 47-65, doi: 10.2478/v10018-012-0013-y.
Sośnica, K., Jäggi, A., Thaller, D., Dach, R., Beutler G. (2014). Contribution of Starlette, Stella, and AJISAI to the SLR-derived global reference frame. J Geod 88(8): 789-804, doi: 10.1007/s00190-014-0722-z.
Sośnica, K. (2014). Determination of Precise Satellite Orbits and Geodetic Parameters using Satellite Laser Ranging. PhD thesis of the Faculty of Science of the University of Bern.
